Attention Mechanism " target="_blank" title="Attention Mechanism" rel="noopener" data-mce-href="http:// Attention Mechanism ">http:// Attention Mechanism
Attention, Learn to Solve Routing Problems!
The recently presented idea to learn heuristics for combinatorial optimization problems is promising as it can save costly development. However, to push this idea towards practical implementation, we need better models and better ways of training. We contr
arxiv.org
Abstract
최근에 조합 최적화 문제를 위한 휴리스틱을 학습하는 아이디어가 제시되었다. 하지만, 이 아이디어를 실제 구현으로 밀어붙이기 위해서는 더 나은 모델과 훈련 방법이 필요하다.
- 포인터 네트워크보다 이점이 있는 Attention 계층을 기반으로 한 모델
- REINFORCE를 사용하여 간단한 결정론적 탐욕적 롤아웃을 기반으로 하는 기본값과 함께 훈련하는 방법
최근 학습된 휴리스틱을 대폭 개선하여, 최대 100개 노드의 문제에 대해 최적의 결과에 가까워지는 여행 판매원 문제(TSP)를 해결한다. 동일한 하이퍼파라미터를 사용하여, 차량 경로 문제(VRP), 오리엔티어링 문제(OP) 및 (확률적 변형의) 상금 수집TSP(PCTSP)을 학습하며, 다양한 베이스라인을 뛰어넘고 매우 최적화된 알고리즘에 가까운 결과를 얻었다.
1. Introduction
이 논문은 기계 학습 알고리즘이 다양한 작업을 해결하기 위해 알고리즘 엔지니어링에서 인간을 대체한 현재 상황을 배경으로 한다. 특히, 딥 뉴럴 네트워크(DNNs)가 컴퓨터 비전, 음성 인식, 기계 번역, 이미지 캡셔닝 등에서 고전적 접근 방식을 능가함으로써 데이터로부터 학습하는 방식의 성공을 강조하고, 강화 학습(RL) 환경과 상호작용하며 결정을 내리는 알고리즘을 학습할 수 있는 능력을 제공한다.
2. Attention Model
- Attention Model을 TSP 상황에 적용하려면 input, mask, decoder, context를 설명해야 한다. 각 TSP문제의 한 인스턴스를 $s$라는 graph형태롤 표현하고, 그 안의 각각의 $n$개의 노드에 대한 feature를 $x_{i}$로 나타낸다.
- 모든 순열에 대한 솔루션 $\pi = (\pi_{1}, \pi_{2},...,\pi_{n})$에 대해 stochastic policy $p(\pi|s)$ 은 매개변수 $\theta$에 대해 다음과 같이 표현된다.
$$p_{\theta }(\pi|s) = \prod_{i=1}^{n}p_{\theta }(\pi_{t}|s,\pi_{1:t-1})$$
Encoder는 모든 input node를 가중치 학습하여 embedding하고, decoder는 위 식의 우측 항의 연산을 $\pi$에 의해 sequential하게 내놓는 역할을 한다. 이 때, TSP는 최초 노드로 들어가야하고, 현재 방문한 노드에 대한 정보를 가지고 있어야하므로, 이 두 정보가 context node(vector)와 함께 decoder에 들어간다
2.1. Encoder
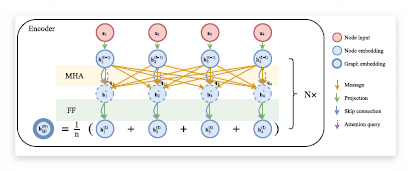
Encoder는 Transformer의 구조에서 positional encoding을 뺀 형태다. 이 때 처음 input(2D TSP에서는 $d_{x} = 2$)은 linear projection을 통해 $d_{h}$ 차원으로 embedding 된다. $W$: 가중치, $b$: bias라고 한다면
$$h_{i}^{(0)} = W^{x}x_{i} + b^{x}$$
이후 N개의 multi-head attention layer를 거치게 되는데 이를 통해 나온 각 노드 $h_{i}^N$에 대해 mean을 취한 $\overline{h}_{i}^{N}$와 함께 decoder에 들어가게 된다.
- Batch Normalization과 Skip Connection을 더한 수식
$$\hat{h}_{i}^{N}= BN^{l}(h_{i}^{(l-1)}+ MHA_{i}^{l}(h_{1}^{(l-1)},...,h_{n}^{(l-1)}))$$
$${h}_{i}^{(l)}= BN^{l}(\hat{h}_{i}+ FF^{l}(\hat{h}_{i}))$$
2.2. Decoder

Decoder는 Encoder에 의한 embedding과 이전 자신의 output을 통해(embedding된) output을 출력한다. 이때 Decoding Context를 나타내기 위해 context node를 사용한다.
- Context Embedding
- 시점 $t$에서 decoder의 context는 encoder와 $t$까지의 output에 의해 나타낸다. 이를 수식으로 나타내면, 마지막 output node와 첫 node를 같이 넣어 context를 만든다. $t=1$에 대해서는 $d_{h}$ 차원 파라미터로 $v_{1}$ 과 $v_{f}$를 사용한다.$${h}_{c}^{(N)} = \begin{cases}
& [\overline{h}^{(N)}, h_{\pi _{t-1}}^{(N)}, h_{\pi _{1}}^{(N)}] \;\;\;\;\;(t>1)\\
& [\overline{h}^{(N)}, v_{1}, v_{f}] \;\;\;\;\;\;\;\;\;\;\;\;\,(t=1)
\end{cases}$$ - ${h}_{c}^{(N)}$ 은 (3 x $d_{h}$) 차원 벡터이다. 이는 encoder로부터 나왔던 embedding $h_{i}^{(N)}$와 함께 multi-head attention을 진행 $$q_{(c)} = W^Qh_{(c)}\;\;\;\;\;\;k_{i}=W^kh_{i}\;\;\;\;\;\;v_i = W^vh_i$$
- 이를 통해 모든 노드의 query,key에 대해 다음과 같이 나타낼 수 있다. $$u_{(c)j} = \begin{cases}
& \frac{q_{(c)}^{T}k_{j}}{\sqrt[]{d_{k}}} \;\;\;\;\;\; (j\neq \pi_t^{'})\\
& -\infty
\end{cases}$$ - 이를 softmax하여 v_i와 곱한다. 이 때 M개의 head로 나눠 연산한다. $$h'_{(c)} = \frac{e^{u_{(c)j}}}{\sum_{j'} e^{u_{(c)j'}}}$$$$MHA_{(c)}(h_{1},h_{2},...,h_{n}) = \sum_{1}^{M}W_{m}^{O}h'_{(c)m}$$
- 시점 $t$에서 decoder의 context는 encoder와 $t$까지의 output에 의해 나타낸다. 이를 수식으로 나타내면, 마지막 output node와 첫 node를 같이 넣어 context를 만든다. $t=1$에 대해서는 $d_{h}$ 차원 파라미터로 $v_{1}$ 과 $v_{f}$를 사용한다.$${h}_{c}^{(N)} = \begin{cases}
- Calculation of log-probabilities$$u_{(c)j} = \begin{cases}
- Decoder의 마지막 layer는 $p_{\theta }(\pi_t = i|s, \pi_{1:t-1})$를 구하기 위해 single attention head를 통한 attention을 진행. 이 때 기존의 NCO에서 사용한 clipping 사용 $$u_{(c)j} = \begin{cases}
& C \times tanh(\frac{q_{(c)}^{T}k_{j}}{\sqrt[]{d_{k}}}) \;\;\;\;\;\; (j\neq \pi_t^{'})\\
& -\infty
\end{cases}$$ - 이를 softmax를 통해 probability처럼 사용 $$p_i = p_{\theta }(\pi_t = i|s, \pi_{1:t-1}) = \frac{e^{u_{(c)j}}}{\sum_{j'} e^{u_{(c)j'}}}$$
- Decoder의 마지막 layer는 $p_{\theta }(\pi_t = i|s, \pi_{1:t-1})$를 구하기 위해 single attention head를 통한 attention을 진행. 이 때 기존의 NCO에서 사용한 clipping 사용 $$u_{(c)j} = \begin{cases}
3. Reinforce with Greedy Rollout Baseline
- 기존의 REINFORCE를 진행하나 이 때, baseline을 구하는데 있어, exponential moving average나 critic을 통해 구하지 않음 $$\bigtriangledown L(\theta |s) = E_{p_{\theta}(\pi|s)}[L(\pi)-b(s))\bigtriangledown logp_{\theta}(\pi|s)]$$
- Determining the baseline policy
- 이는 baseline으로 DQN에서 target Q network정하던 것처럼 fixed policy $p_{\theta^{BL}}를 정하는데, 이는 t-test를 통해 기존보다 향상됨이 검증된 policy를 사용함
- Algorithm

Baseline을 구하는 부분 외에는 기존 Reinforce 알고리즘과 동일