TaeKyoung's Study Blog

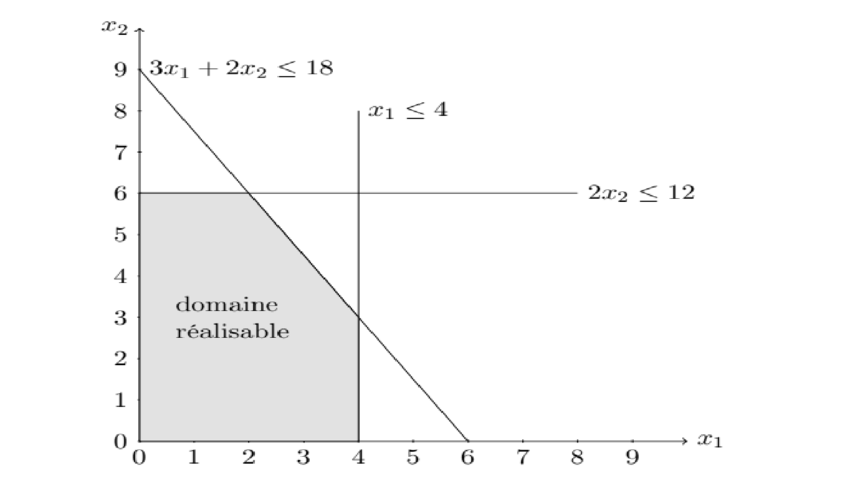
지난 주에 심플렉스 테이블의 행렬형 구조를 다루면서 초기테이블에 따라 특정 단계의 테이블 (혹은 최종 테이블)이 어떻게 구성되고, 변화하는지에 대해 살펴보았다. 그리고 '최적해 사후 분석' 포스팅에서 목적함수나 제약식의 변화에 따라 최적해가 변하는 민감도 분석에 대해서 살짝 다뤘었다. 오늘 포스팅에서는 심플렉스 테이블을 활용한 민감도 분석의 확장형 모델에 대해서 학습해보도록 하겠다. 심플렉스 테이블의 행렬형 구조" target="_blank" rel="noopener" data-mce-href="http://심플렉스 테이블의 행렬형 구조">http://심플렉스 테이블의 행렬형 구조 [경영과학] 심플렉스 테이블의 행렬형 구조지금까지 심플렉스 방법을 소개하면서 대수적 형태와 표의 형태로 설명하였다. 심플렉스..

지금까지 심플렉스 방법을 소개하면서 대수적 형태와 표의 형태로 설명하였다. 심플렉스 방법을 행렬형으로 검토하면 더 깊은 통찰을 얻을 수 있다. 다음은 앞서 다뤘던 예제 문제이다.$$\begin{align*}\text{Maximize} \quad & Z = 3x_1 + 5x_2 \\\text{Subject to} \quad & x_1 \leq 4 \\ & 2x_2 \leq 12 \\ & 3x_1 + 2x_2 \leq 18 \\ & x_1 \geq 0, \quad x_2 \geq 0\end{align*}$$ 이 표준형 예제를 행렬형으로 표기하면 다음과 같다.\[ \begin{aligned} ..

OR에서 문제의 시나리오가 바뀔 경우 최적해를 다시 찾아야 하는 경우가 있는데, 이를 효율적으로 해결하는 것은 매우 중요한 과제이다. 시나리오가 바뀐다는 것은 다음을 의미할 수 있다.제품 생산량당 얻는 단위 이득의 변화허용된 자원의 양의 한계치가 변화이 때 문제를 처음부터 다시 풀 수도 있겠지만, 그러기보다는 이전 문제의 최적해와 바뀐 문제의 최적해가 서로 멀리 떨어져 있지 않을 것이라 가정하고 접근하는 재최적화 방법을 쓰는 것이 일반적이다. 아래와 같은 예제가 있다고 하자. 각 결정변수는 제품 1,2를 각각 얼마나 생산할 지를 나타내는 변수이고, 목적함수의 계수는 제품 1, 2의 단위 생산량 당 이득으로 생각할 수 있다. 각각의 제약식은 제품1, 2를 생산하는데 드는 자원1,2,3에 대한 제약으로, 계..

비표준형 모형지금까지 우리는 표준형 (기능제약식이 모두 $\leq$ 이며, 모든 변수가 비음이며 목적함수는 최대화) 이라는 가정 하에서 심플렉스 방법을 적용하였다. 이번 포스팅에서는 이러한 표준형이 아닌 모형 (기능제약식이 등식이거나 $\geq$ 형태인 경우)를 다룰 것이다. 기능 제약식이 (= 또는 $\geq$형태)인 경우의 문제는 초기해를 찾는 것에서 발생한다. 표준형태에서는 여유변수를 초기 기저변수로 잡으면 각 변수의 값이 비음이 되므로 초기해가 편리하게 찾아졌다. 그러나 비표준 형태에서는 여유변수를 두어도 비음을 만족시키지 못할 가능성이 있으므로 추가적인 접근법을 도입해야 한다. 그 접근법을 인공변수라고 한다. 빅 $M$ 방법 등호 제약식 문제$$\begin{align*}\text{Maximize..

What is Dynamic Programming?Dynamic Programming (동적 계획법)이란 복잡한 문제를 다음과 같은 방법으로 푸는 것을 말한다.Sub-Structure : 상위 문제를 하위 문제로 쪼갠다Table-Structure : 각 하위 문제를 해결한 후 계산된 해를 테이블에 저장하여 여러 번 재사용Bottom-up Computation : 작은 하위 문제의 해를 결합하여 더 큰 하위 문제를 해결하고 원래 문제에 접근동적 계획법은 다음과 같은 조건 하에서 풀린다.Optimal Sub-structure : 원 문제의 최적해는 하위 문제들의 최적해들로부터 도출된다Overlapping Sub-problems : 동일한 하위 문제의 해가 반복적으로 필요하므로 계산된 해를 테이블에 저장하여 ..

심플렉스 방법의 대수학적 접근이전 포스팅에 이어서 심플렉스 방법의 개념의 요점을 정리하도록 하겠다. 전에 다뤘던 예제를 다시 가져와 보자.$$\begin{aligned} \text{Maximize} \quad & z \\ \text{Subject to} \quad & z - 3x_1 - 5x_2 = 0 \\ & x_1 + x_3 = 4 \\ & 2x_2 + x_4 = 12 \\ & 3x_1 + 2x_2 + x_5 = 18 \\ & x_j \geq 0, \quad j = 1, 2, 3, 4, 5 \end{aligned} $$ 참고로, 이..

심플렉스 방법의 핵심심플렉스 방법은 대수적 절차 중 하나이다. 그러나 내재된 개념은 기하학적이다. 이러한 기하학적 방법을 이해하면 심플렉스 방법이 어떻게 운영되는지와 왜 그렇게 효율적인지에 대해 강한 통찰력을 갖게 된다. 다음과 같은 예제를 살펴보자심플렉스 방법의 핵심심플렉스 방법은 대수적 절차 중 하나이다. 그러나 내재된 개념은 기하학적이다. 이러한 기하학적 방법을 이해하면 심플렉스 방법이 어떻게 운영되는지와 왜 그렇게 효율적인지에 대해 강한 통찰력을 갖게 된다. 다음과 같은 예제를 살펴보자$$\begin{align*} \text{Maximize} \quad & z = 3x_1 + 5x_2 \\ \text{Subject to} \quad & x_1 \leq 4 \\                     ..

What is Optimization? Optimization(최적화)란 해결해고자 하는 문제를 정해진 제약조건 내에서 최적의 결과로 결정하는 것을 의미한다. 즉, 어떠한 상황 속에서 최대의 성능을 내도록 문제를 푸는 과정을 최적화라고 한다. 딥러닝에서의 최적화 역시 모델이 최적의 성능을 발휘할 수 있도록 파라미터들을 조정하는 것을 의미한다. 이전에 최적화 기법으로 "Full - Batch", "Stochastic", "Mini-Batch-Stochastic" Gradient Descent 에 대해서 배운 적이 있다. 이번 포스팅에서는 이 기법들 외에 모델이 더 안정적으로 수렴할 수 있도록 하는 최적화 기법들에 대해서 다룰 생각이다. Momentum (관성)모델에 입력될 데이터의 initialize 지점..

Activation Function 이란?Activation Function $\sigma$ 란 layer 와 layer 사이에 위치한 non-linear function (비선형 함수) Activation Function은 왜 필요한가?? Non-Linear 한 activation function을 사용함으로써 뉴럴넷은 non-linear한 decision boundary를 그릴 수 있기 때문이다. 그리고 linear한 activation function을 사용하면 아무리 많은 layer를 쌓아도 Single Layer Neural Network에 불과하다. 그 이유에 대해서 알아보도록 하자.  이미지의 예시를 살펴보자. Output $y$에 대해 정리해보면 다음과 같다. $\begin{aligned}..

이전 포스팅에서 Gradient Descent에 대한 기본적인 내용을 다룬 바 있다. 오늘은 이와 이어지는 내용으로 Gradient Descent의 더 심화된 버전을 다뤄볼 생각이다. 이번 포스팅의 내용에서는 쉬운 이해와 간결성를 위해 Activation Function은 배제하고 생각하겠다. 경사하강법" target="_blank" rel="noopener" data-mce-href="http://경사하강법">http://경사하강법 [딥러닝] Gradient Descent (경사하강법)1. ML as an Optimization Problem기계학습이 해야 할 일을 식으로 정의하면, 주어진 cost function $J(\theta)$에 대해, $J(\theta)$를 최소로 하는 $\hat{\theta..