연속형 확률분포
연속형 확률분포란 확률변수 $X$가 주사위 눈의 수, 카페에 도착하는 손님의 수 처럼 이산형 확률변수인 게 아니라 대한민국 남성의 평균 키, 경기도 주민의 평균 소득수준과 같이 값이 연속적인 경우의 확률분포를 의미한다. 오늘은 대표적인 연속형 확률분포함수인 균일분포 (Uniform Distribution), 지수분포 (Exponential Distribution), 감마분포 (Gamma Distribution), 와이블 분포(Weibull Distribution) 등을 소개할 예정이다.
1. Uniform Distribution (균일분포)
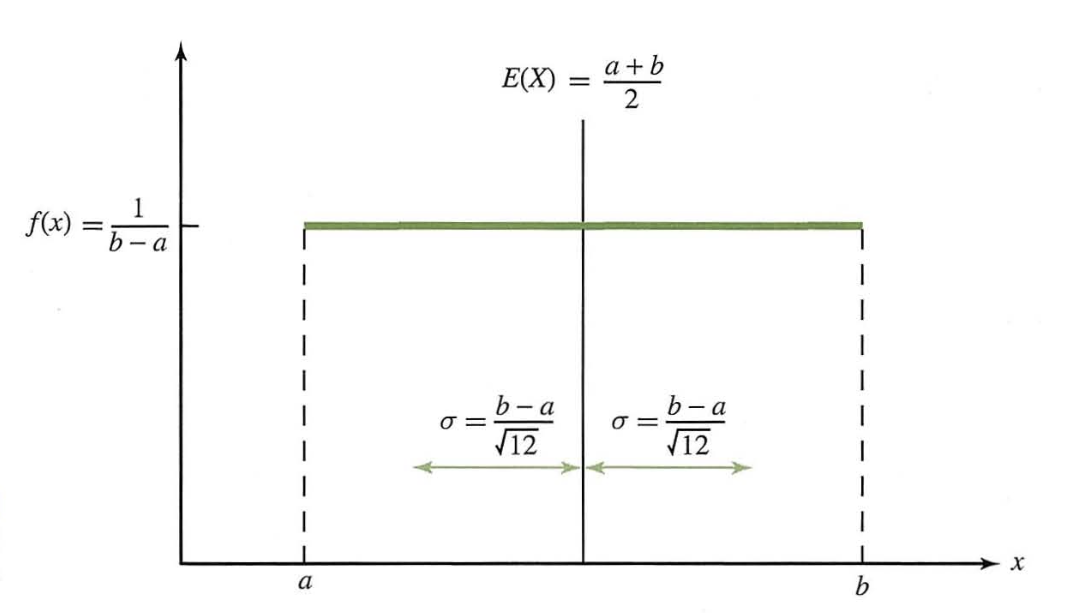
가장 단순한 형태의 연속확률분포이다. 균일분포는 두 점 a,b 사이에 평행한 확률분포로, $X \sim U(a,b)$로 표시되며 함수 아래의 면적이 1이어야 하므로 구간 $[a,b]$에서 PDF는
$$f(x) = \frac{1}{b-a}$$
이 되며 그 외의 구간은 $f(x) = 0$이 된다. 이때, CDF는
$$F(x) = \int_{a}^{x} f(x)dx = \frac{x-a}{b-a}, \quad (a ≤ x ≤ b)$$
이를 바탕으로 다른 통계량들을 구해보면,
$$E(X) = \int_{a}^{b} xf(x)dx = \frac{a+b}{2}$$
$$E(X^2) = \int_{a}^{b} x^2f(x)dx = \frac{a^2 + ab + b^2}{3}$$
$$Var(X) = E(X^2) - E(X)^2 = \frac{(b-a)^2}{12}$$
2. Exponential Distribution (지수분포)
지수분포는 $x ≥ 0$의 상태공간을 가지며, 종종 고장이나 대기시간 혹은 도착시간을 모형하기 위하여 사용된다. 그 PDF는 모수 $\lambda$에 의하여 결정된다.
$$f(x) = \lambda e^{-\lambda x} \quad (x ≥ 0)$$
이며 모든 $x ≤ 0$에 대해서는 $f(x) = 0$이 된다.
$$F(x) = \int_{0}^{x} f(x)dx = 1 - e^{-\lambda x}$$
모수 $\lambda$를 가지는 지수분포들의 통계량은
$$E(X) = \int_{0}^{\infty} x f(x)dx = \frac{1}{\lambda}$$
$$E(X^2) = \int_{0}^{\infty} x^2 f(x)dx = \frac{2}{\lambda^2}$$
$$Var(X) = E(X^2) - (E(X))^2 = \frac{1}{\lambda^2}$$
즉, 지수분포의 표준편차는 기댓값과 동일하다.
◈ 지수분포의 무기억성 (Memoryless Property)
지수분포의 중요한 특성 중 하나는 무기억성이라는 특성이다. 무기억성이란 현재를 기준으로 앞으로 일어날 사건들에 대한 확률분포는 과거의 분포들에 의존하지 않는다는 것이다. 즉, 만약 $X$가 모수 $\lambda$의 지수분포라면, 임의의 $x_0 \in X$에 대해, $X - x_0$역시 모수 \lambda인 지수분포를 따른다는 것이다. 다음과 같이 증명이 가능한데,
$$P(X ≥ x) = 1 - P(X ≤ x) = 1 - F(x) = e^{-\lambda x}$$
이고, $Y$를 $x_0$이후의 경과시간으로 정의하면,
$$P(Y ≥ y) = P(X ≥ x_0 + y | X ≥ x_0) = \frac{P(X ≥ x_0 + y)}{P(X ≥ x_0)} = \frac{e^{-\lambda (x_0 + y)}}{e^{-\lambda x_0}} = e^{-\lambda y}$$
이므로 $Y$는 모수 $\lambda y$의 지수분포를 따른다.
◈ 포아송 과정
확률과정은 일련의 랜덤 사건으로 간주될 수 있다. 특히 단순한 확률을 시간에 따라 발생하는 연속적인 사건으로 간주되며 그 경우 확률 과정은 구간의 확률분포를 명시함으로써 구체화될 수 있다. 모수 $\lambda$를 갖는 포아송 과정은 이러한 인접한 두 사건의 발생 시간이 서로 독립이며 모수 $\lambda$를 따르는 지수분포를 따르는 확률변수로 정의되는 과정이다.
따라서 포아송 과정에서 단위시간 당 발생하는 사건의 수를 모수 $\lambda$로 두면, 두 사건 사이의 평균 time-interval은 $\frac{1}{\lambda}$로 정의된다. 또한 길이 $t$를 가지는 고정된 시간 구간에 발생하는 사건의 수는 $\lambda t$가 된다.
$$X \sim (\lambda t)$$

3. Gamma Distribution (감마 분포)
감마분포는 신뢰성 이론과 같은 분야에서 주로 사용되며, 포아송 과정을 분석하는데 사용되기도 한다. $x ≥ 0$의 상태공간에 대하여 감마분포의 확률밀도함수는
$$f(x) = \frac{\lambda^k x^{k-1} e^{-\lambda x}}{\Gamma (k)}$$
감마분포는 모수 $k ≥ 0$과 $\lambda ≥ 0$에 의해 결정되며, 감마함수는 함수 아래 면적을 1로 만들기 위해 필요하다.
[감마함수]
$$\Gamma (k) = \int_{0}^{\infty} x^{k-1} e{-x} dx$$
로 정의되며, $\Gamma(1) = 1$, $\Gamma(\frac{1}{2}) = √π$이다.
일반적으로 $\Gamma (k) = (k-1)\Gamma(k-1)$이며, $n$이 양의 정수일 때 $\Gamma(n) = (n-1)!$이다. 모수들에 대한 통계량은 다음과 같다.
$$E(x) = \frac{k}{\lambda}, \;\; Var(X) = \frac{k}{\lambda^2}$$
4. Weibull Distribution (와이블 분포)
감마분포로부터 도출되는 와이블분포는 고장시간이나 대기시간을 모형화하는 데 사용된다.
$$f(x) = a \lambda^a x^{a-1} e^{{-\lambda x}^{a}} \quad (x ≥ 0)$$
로 정의된다.
와이블분포의 누적분포함수는
$$F(x) = 1 - e^{{\lambda x}^{a}}$$
로 표현되며, $E(X) = \frac{1}{\lambda} \Gamma (1 + \frac{1}{a})$이다.
'Mathematics > 통계학' 카테고리의 다른 글
| [확률] 4. Discrete Probability Distributions (1) | 2024.05.03 |
|---|---|
| [확률] 3. Expectations, Variances, Standard Deviations (기댓값, 분산, 표준편차) (1) | 2024.04.10 |
| [확률] 2. Random Variables (확률 변수) (3) | 2024.04.04 |
| [확률] 1. Probability Theory (확률론) (1) | 2024.03.17 |