[ADA] 데이터 기반 의사결정

의사결정 3요소

의사결정이란 여러 대안이 존재할 때, 그 대안 중 하나를 선택하는 지각 활동을 의미한다. 모든 의사결정 과정은 하나의 최종 선택을 갖게 되며, 이 선택으로 인해 모든 사항에 대한 행동과 선택이 정해지므로 적절한 의사결정은 매우 중요하다고 할 수 있다.

 

데이터 분석에서도 분석 결과를 통해 적절한 의사결정을 하는 것이 매우 중요한데, 오늘은 이 의사결정의 기반이 되는 3가지 요소인 문제정의, 분석기획, 성능검증에 대해 알아보고, 이 요소들이 어떻게 쓰이는 지 알아보도록 하겠다.

 

 

1) 문제 정의 : 현실에서 어떤 문제를 풀지 정하는 것

• 우리는 일상 상황 매 순간마다 의사결정이 필요한 문제들을 해결하고 있고, 마찬가지로 비즈니스 연구 등에서도 모든 순간들에는 해결해야 할 문제 존재

 

2) 분석 기획 : 풀어야 하는 문제를 데이터 분석 과정에서 어떻게 증명할 것인지 기획

• 데이터 분석 모든 단계에서 가장 중요한 것이 문제 정의를 증명하고 해결해 나가는 분석기획 단계
• 고민해야 할 문제 11가지
  1.  내가 풀어야 할 문제가 무엇인지, 명확하게 제시할 수 있나?
  2. 사람들은 그 문제를 풀기 위해 어떤 해결책을 시도하는가?
  3. 데이터로 그 문제를 해결하려면 어떤 데이터가 필요한가?
  4. 해당 데이터를 수집하기 위해서는 어떤 방식을 활용할까?
  5. 수집한 데이터를 바로 사용 가능한가?
  6. 데이터 수집 대상과 기간은 어떻게 정할 것인가?
  7. 수집할 데이터 양은 어떻게 정할 것인가?
  8. 수집된 데이터를 어떻게 정제해서 사용할 것인가?
  9. 정제된 데이터를 가지고 어떤 실험을 할 것인가?
  10. 데이터 분석 결과, 어떤 인사이트를 도출할 수 있는가?
  11. 도출된 인사이트를 실제 비즈니스에 적용할 수 있을 것인가?

 

3) 성능 검정 : 데이터 분석 과정에서 도출된 의사결정 후보들을 현실에서 검증하는 것

• 데이터 분석 산출물이 현실에서 검증되지 못한다면 의미없는 데이터 분석 될 것

 

통계추론 기반 의사결정 

1) 통계추론 : 샘플을 분석하여 모집단의 특성을 추론하고 신뢰성 검정 하는 것

• 최근엔, 보유한 데이터를 샘플, 보유하지 못한 미래 데이터를 모집단으로 인식하는 경향 있음
• 샘플로 모집단을 추정하기 때문에, 샘플의 특성이 모집단을 잘 반영해야 함
• 샘플의 기초통계로 데이터 분포 확인하고, 분포에 따라 분석 방법론 달라짐
• 통계량 (Statistic) : 샘플의 특성을 측정한 수치
• 모수 (Parameter) : 모집단의 특성을 측정한 수치
• 샘플 오차 (Sampling Error) : 모집단의 특성과 샘플의 특성의 차이
• 모평균 추론 시 여러 번의 샘플 추출의 통해 평균 통계량으로 추정 (절대 샘플 평균이 모평균을 의미하지 않음!)

 

2) 중심극한정리 (Central Limit Theorem) : 모집단에서 추출한 표본들의 평균의 분포가 표본의 개수가 커질수록 정규분포를 따른다.

 

1. 데이터가 어떤 형태이든 (모집단) 어떠한 사건이라도 반복적으로 추정하면 (샘플) 정규분포!

 

출처: https://ko.wikipedia.org/wiki/%EC%A4%91%EC%8B%AC_%EA%B7%B9%ED%95%9C_%EC%A0%95%EB%A6%AC

 

 

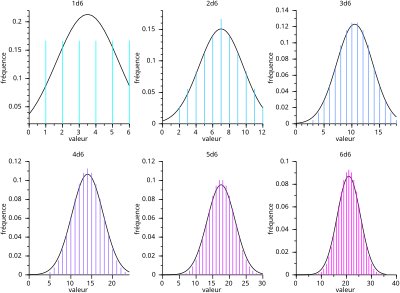
(2) 큰 수의 법칙 : 실험 반복 횟수가 증가하면 기대되는 발생확률 (통계적 확률)은 이론적 수치 (수학적 확률)과 같아짐

• 표본을 여러 번 추출해서 그 평균을 구하는 횟수가 많아질수록 그 평균들은 모평균과 같아질 것을 기대함 (기댓값을 의미함)
• 표본을 여러 번 추출해서 그 오차를 구하는 횟수가 많아질수록 최종 오차 감소 $$\bar{X}  \sim (\mu, \frac{\sigma^2}{n})$$

 

가설검정 기반 의사결정

가설 검정 3단계

(1) 가설 설정: 

• 귀무 가설 (Null Hypothesis) : 현재의 상황이나 통념, 내가 증명하고자 하는 것에 반대되는 가설
• 대립 가설 (Alternative Hypothesis) : 새로운 현상이나 주장, 내가 증명하고자 하는 가설

 

(2) 검정 통계량: 귀무가설과 대립가설을 비교하기 위한 통계량 (점추정)

• 귀무가설과 대립가설에 차이가 없다면 검정통계량은 0에 가까울 것
• 귀무가설과 대립가설에 차이가 있다면 검정통계량은 0보다 커질 것
• 검정통계량에 두 집단의 차이를 사용하는 이유 : 두 집단을 각각 분석하기보다 차이만 분석하면 훨씬 단순 (통계량 2개 -> 1개)
• 신뢰구간 (Confidence Interval) : 검정통계량을 여러 횟수로 추정한 범위 (구간추정)
• 유의수준 (Significance Level, $\alpha$) : 분석가가 설정한 오류 최대 허용범위
  • 유의 수준 5% ($\alpha = 0.05$) : 귀무가설이 틀렸다고 주장할 오류가 5%임을 의미

여기서 잠깐!
나는 유의수준이라는 개념을 처음 배울 때, 개념을 완벽하게 이해하는 데 시간이 좀 걸렸어서, 내가 나름 해석한 유의수준의 의미를 설명하자면, 유의수준은 귀무가설이 참이라는 가정 하에, 그것을 기각을 했을 때, 그 결정이 틀렸을 확률이라고 생각하면 된다. 즉, 유의수준이 작아질 수록, '귀무가설 기각' 이라는 결정이 틀릴 확률이 작아지므로, 더 확실하게 귀무가설을 기각할 수 있는 것이다. 같은 맥락으로 신뢰수준이 높아지는 것이다.

 

 

(3) 의사결정

• 유의확률 (p-value) : 직접 실험을 통해 계산한 오류치
  • 유의확률 (p-value) > 유의수준 ($\alpha$) : 대립가설 발생확률 > 허용 오류 한계, 즉 귀무가설 기각 불가!
  • 유의확률 (p-value) < 유의수준 ($\alpha$) : 대립가설 발생확률 < 허용 오류 한계, 즉 귀무가설 기각!