1. Yield Curves (수익률 곡선)
모든 채권의 수익률은 고정수익증권 시장에서 서로 같이 움직이는 경향이 있다. 그러나 모든 채권의 만기수익률이 동일하지는 않다. 왜냐하면 채권에는 다양한 질적인 등급이 있기 때문이다.
신용 등급이 높은 채권 (예: AAA)은 지급 조건이 동일하다 하더라도 등급 B의 채권보다 가격이 비싸기 때문에 수익률이 낮다. 신용 등급이 높은 채권은 부도가 날 가능성이 적다는 것을 의미하므로 안정성이 높은 채권일수록 높은 수익률을 보장하기 어렵다는 뜻이기도 하다. 그러나 다양한 채권수익률이 존재하는 것을 신용 등급만으로는 설명할 수 있다.
채권 수익률의 차이는 만기까지의 기간으로도 설명이 가능하다. 일반적으로 같은 등급의 채권의 경우, 장기채권이 단기채권보다 수익률이 높다.

이미지처럼 점차 증가하는 곡선의 모양이 정상적인 곡선의 형태이다. 그러나 간혹 장기채권의 수익률이 단기채권보다 적게 나타나는 경우가 있는데, 이를 '역전된 수익률 곡선' 이라고 한다. 이러한 현상은 단기 채권의 금리가 빠르게 상승하 때 나타나는데, 이때 투자자들은 이를 일시적인 현상이라 여겨 장기채권을 더 많이 보유하게 된다. 그렇게 되면 장기채권의 가격이 높아져 상대적으로 단기채권에 비해 수익률이 낮아진다.
특정 채권을 연구할 때, 수익률과 만기를 알아내는 것과 이로부터 그 채권의 수익 곡선에서 어느 위치에 있는지 알아내는 것은 위험을 분류하는 데 있어 중요하다.
2. Term Structures (기간구조)
기간구조이론은 수익률을 일단 배제하고 이자율에 초점을 둔다. 예를 들어, 예금의 경우 수시로 찾을 수 있는 요구불예금보다 3년 기간의 정기예금의 이자율이 더 높다는 것을 알고 있다. 즉, 보유 기간에 따른 이자율의 변화가 이자율 기간구조의 기본적인 아이디어라고 할 수 있다.
2.1. Spot Rate (현물 이자율)
현물 이자율은 기간구조를 정의하는 가장 기본적인 이자율이다. 현물이자율 $s_t$는 연 단위로 표현되며, 현재 $(t=0)$부터 기간 $t$까지 돈을 보유하는 것에 부과되는 연 이자율이다. 즉, $s_1$은 1년간 보유 시 지급되는 이자율이고, $s_2$는 2년간 보유 시 지급되는 이자율이다. 따라서 은행에 원금 $A$를 정기예금 시, $t$년 후 받게 될 원리금은
$$(1 + s_t) ^ t A$$
위는 연 단위 복리계산을 가정 했을 때의 식이고, 이자율 지급기간에 따라 다음과 같이 표현되기도 한다.
(a) 연간 복리 계산 :$ (1 + s_t)^t$
(b) 연간 m회 복리 계산 : $ (1 + \frac {s_t}{m}) ^ {mt}$
(c) 연속 복리 계산 : $e^{s_t t}$

2.2. 할인요소와 현재가치
현물 이자율이 결정되면 각 시점에서 할인 요소 $d_t$가 정의될 수 있다. 기간별 복리 계산에 따른 할인요소는 다음과 같다.
(a) 연간 복리 계산 : $d_k = \frac {1}{(1+s_k)^k}$
(b) 연간 m회 복리 계산 : $d_k = \frac {1}{(1 + \frac{s_k}{m})^{mk}}$
(c) 연속 복리 계산 : $ d_t = e^{-s_t t}$
할인 요소는 미래 현금흐름을 상응하는 현재가치로 변환시켜 준다. 따라서 어떤 현금흐름 $(x_0, x_1, x_2, \cdots, x_n$이 주어진다면, 현재가치는 아래와 같이 주어진다.
$$PV = x_0 + d_1x_1 + d_2x_2 + \cdots + d_nx_n$$
2.3. 현물 이자율 결정
현물 이자율 곡선을 결정하는 쉬운 방법은 다양하 만기의 무이표채권들의 가격을 조사하면 된다. 그러나 현실적으로 무이표채권은 매우 드물기 때문에, 이와 같은 방법은 현실적이지 못하다.
따라서 무이표채권 없이 이표지급 채권으로도 현물 이자율 곡선을 결정할 수 있다. 우선 단기채권의 현물이자율을 먼저 구한 후, 장기채권으로 확대하면서 장기의 현물이자율 곡선을 결정할 수 있다. 우선, 1년 만기 단기채권 이자율로 $s_1$을 결정한다.
$$P_1 = \frac {C + F} {1 + s_1}$$
이렇게 $s_1$을 구한 후, 2년 만기 채권을 고려하여 $s_2$를 구한다.
$$P_2 = \frac {C}{1 + s_1} + \frac{C + F} { (1 + s_2)^2}$$
이러한 과정을 계속 반복하다 보면 만기 $N$년인 채권에 대해서는 다음과 같이 현재가치를 구할 수 있다.
$$P_N = \sum_ { i = 1}^{N} \frac {C}{ (1 + s_i) ^ i} + \frac{F}{(1 + s_N)^N}$$
◈ 뺄셈 방식
채권의 현물 이자율은 뺄셈방식이라는 방법을 통해서도 구할 수 있는데, 만기는 같고 이표이자율이 다른 두 채권으로부터 같은 가치의 무이표 채권 포트폴리오를 구성하는 방식이다.


이렇게 두 채권의 보유 비율을 다르게 설정하여 이표 이자 현금 흐름 부분을 상쇄시킬 수 있다. 작업을 수행하고 나면 다음과 같이 같은 가치의 무이표채권과 동일한 가치의 현금 흐름을 생성할 수 있다.

3. Forward Rates (선도 이자율)
현물 이자율을 이용해 또 다른 개념을 도출할 수 있는데 바로 선도 이자율이다. 선도이자율이란 현재 시점에서 동의된 미레 두 시점간의 이자율이다.
예를 들어, 2년동안의 기간을 고려하자. 현물 이자율 $s_1$과 $s_2$가 알려져 있다고 가정하자. 이때, 은행에 1만원을 예금하는 방법은 두 가지가 있다.
1) 1만원을 2년 동안 정기예금한다.
2) 1만원을 1년동안 정기예금 한 후, 1년 후 찾은 돈을 다시 1년 간 정기예금 한다.
이 때, 경우 2)의 두번째 예금은 지금으로부터 1년 후에 시작될 1년 동안의 예금으로, 이 예금의 이자율은 $f$로 미리 정해진 선도이자율이다. 이 때, 1)의 경우와 2)의 경우 2년 후에 돌려받는 현금의 가치는 동일해야 하므로
$$ (1 + s_2)^2 = (1 + s_1)(1 + s_f)$$ 이므로 다음과 같이 선도 이자율 $f$를 얻을 수 있다.
$$ f = \frac {(1 + s_2)^2}{1 + s_1} - 1$$
이제 선도 이자율을 일반화하여 지금 동의된 두 미래 시점 사이의 연 이자율로 정의한다. 이 때, $i$ 시점부터 $j$ 시점까지의 선도 이자율은 $f_{i, j}$로 표현된다.
$$(1 + s_j) ^ j = (1 + s_i)^i (1 + f_{i,j})^{j-i}$$
위 등식의 좌변은 $j$기간 동안 직접 투자할 때의 수익 증가요소를 의미하며, 이 금액은 현물 이자율 $s_j$에 의해 결정된다. 등식의 우변은 먼거 $i$ 기간 동안 투자한 후, 회수된 금액을 $i$년도에서 $j$년도까지 $(j-i)$기간 투자하여 증식시키는 증가 요소에 해당한다.
이 등식을 이용하여 다양한 복리 계산 기간에 따라 선도이자율을 정의할 수 있다.
(a) 연간 복리 계산 : $f_{i,j} = \left( \frac{(1+s_j)^j}{(1+s_i)^i} \right)^{\frac{1}{j-i}} - 1
$
(b) 연간 m회 복리 계산 : $f_{i,j} = m\left( \frac{(1+\frac{s_j}{m})^j}{(1+\frac{s_i}{m})^i} \right)^{\frac{1}{j-i}} - m
$
(c) 연속 복리 계산 : $ f_{i,j} = \frac{s_j j - s_i i}{j - i}$
4. Expectations Dynamics (기대역학)
현물 이자율 곡선 형태에 대한 설명으로 미래 이자율에 대한 그럴듯한 예측 도구가 될 수 있다. 현물 이자율 예측을 위한 기본적인 가정은 현물 이자율 곡선으로 표현된 기대는 실제로 성취될 것이라는 거다. 즉, 이러한 가정에 의해 현재의 현물이자율 곡선으로부터 내년의 현물 이자율 곡선을 예측할 수 있다.
현재의 현물 이자율 곡선 $s_1, s_2, \cdots, s_n$을 통해 내년 현물 이자율 곡선 $s_1 ^{'}, s_2^{'}, \cdots , s_n^{'}$을 예측하려 한다. 현재의 선도이자율 $f_{i,j}$는 내년의 어떤 이자율의 기대로 간주된다.
$$s_{j-1}^{'} = f_{1,j} = \left( \frac{(1+s_j)^j}{(1+s_1)} \right)^{\frac{1}{j-1}} - 1$$
초기의 현물이자율 곡선에 의해 함축되어 있는 미래의 현물 이자율 곡선들은 초기의 현물이자율과 연관된 선도 이자율에 의해 나열될 수 있다. 이와 같은 나열은 아래와 같이 삼각행렬의 모양을 갖는다.
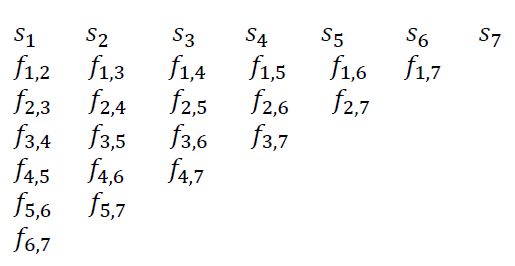
4.1. 할인 요소
또 다른 중요한 개념으로 두 시간 간의 할인 요소 개념이 있다. 이 때, 선도이자율로 표현된 할인요소 식은 다음과 같다.
$$d_{j,k} = (\frac {1} {(1 + f_{j,k})})^{k-j}$$
또한, 시간 순서대로 $i < j < k$ 일 때,
$$d_{i,k} = d_{i,j} d_{j,k}$$
4.2. 단기 이자율
단기 이자율이란 단일 기간 동안의 선도이자율이다. $k$시점에서의 단기 이자율은 따라서 $r_k = f_{k,k+1}$이다. 각 기간의 단기이자율을 안다면 그것들로 기간구조를 모두 얻을 수 있다.
$$(1 + s_k)^k = (1 + r_0)(1 + r_1) \cdots (1+r_{k-1})$$
$$(1 + f_{i,j})^{j-i} = (1 + r_i)(1 + r_{i + 1}) \cdots (1 + r_{j-1})$$
5. Duration (듀레이션)
지난 포스팅에서 소개한 듀레이션 개념은 기간구조 틀에서 확장하 수 있다. 듀레이션은 채권에 대한 이자율 민감도의 척도였으며, 구체적으로 채권의 수익률에 대한 민감도로 개발되었다. 그러나 기간구조 틀에서는 수익률은 기본적인 양이 될 수 없기 때문에 다른 리스크의 척도로 구성할 수 있다.
수익률의 대안으로 우리는 현물 이자율 곡선을 평행 이동함으로써 얻을 수 있다. 즉, 현물 이자율이 모두 어떤 $\lambda$를 더해지는 것만큼 변화할 수 있다.
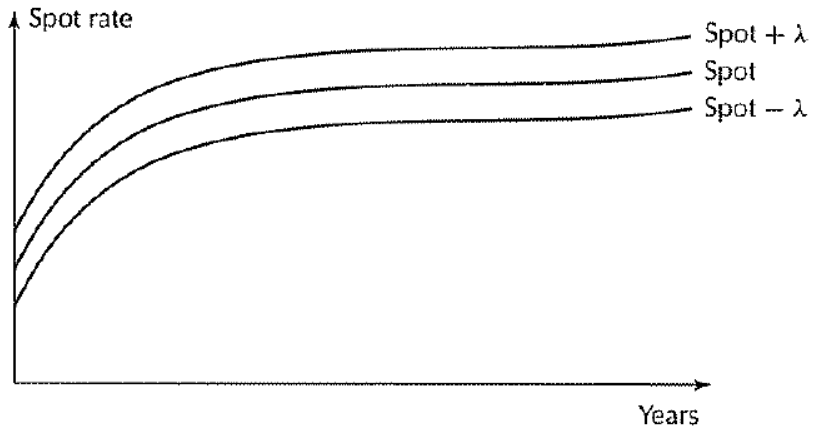
◈ 피셔 - 웨일 듀레이션
연속 복리 계산의 경우 계산이 깔끔하게 표현되므로 이 경우부터 고려한다. $t_n$ 기간의 현금흐름의 현재가치는 다음과 같이 정해진다.
$$PV = \sum_{i=0}^n x_{t_i} e^{-s_{t_i}t_i} $$
그러면 피셔-웨일 듀레이션은 다음과 같이 정의된다.
$$D_{FW} = \frac{1}{PV} \sum_{i=0}^n \frac{t_i x_i e^{-s t_i}}{t_i}$$
이제 수익률 곡선의 평행이동에 대한 가격 (현재가치) 민감도를 고려하자. 임의의 $\lambda$에 대해 가격은 아래와 같다.
$$PV(\lambda) = \sum_{i=0}^n x_{t_i} e^{-s_{t_i} t_i + \lambda} $$
$$\left.\frac{dPV}{d\lambda}\right|_{\lambda=0} = -\sum_{i=0}^n t_i x_i e^{-s _{t_i}t_i}$$
따라서 상대적 가격 민감도는
$$\left.\frac{dP}{d\lambda}\right|_{\lambda=0} = -D_{FW}$$ 와 같다.
'금융공학' 카테고리의 다른 글
| [금융] 거시경제 지표 분석 (4) | 2024.07.20 |
|---|---|
| [금융] 거시 경제와 금융 (3) | 2024.07.20 |
| [Quant] Fixed - Income Security (3) | 2024.03.28 |
| [Quant] Nominal and Effective Interest Rates (0) | 2024.03.24 |
| [Quant] Factors: How Time and Interest Affect Money - Part2 (2) | 2024.03.23 |