Introduction
금리와 관련된 전반적인 금융 시장 내의 현금 흐름은 2장에서 다뤘던 단순한 내용보다 훨씬 복잡하다. 청구서, 어음, 채권, 담보대출 등 더 복잡한 과정으로 현금이 거래되는데, 이 글에서는 이들이 거래되는 시장, 특히 채권의 매매에 따라 현금이 어떻게 움직이는 지에 대해 설명하려 한다.
1. The Market for Future Cash
1.1. Fixed Income Security
- 전통적으로 채권형 증권은 고정적이고 잘 정의된 현금 흐름 흐름을 지급한다.
- 불확실한 것은 채권발행자의 채무불이행 여부
- 일부 고정 수익 증권은 다양한 우발 상황이나 변동 지수에 연동된 현금 흐름을 보장한다. (예: 조정 금리 모기지는 이자율 지수에 연동될 수 있음).
- 일반적으로 고정 수입 증권은 잘 정의 된 우발적 상황으로 인한 변동을 제외하고는 고정 된 현금 흐름 흐름을 가지고 있다.
1.2. Savings and Deposits
- 가장 보편적이고 익숙한 Fixed Income Instrument (고정 수익 상품)
- 상업 은행, 저축 및 대출 기관, 신용 조합에서 제공
1.3. Callable Bonds (콜 채권)
콜 채권은 채권 발행자가 채권이 만기일에 도달하기 전 특정 시점에 채권을 상환할 수 있는 특권을 보유할 수 있는 채권의 한 유형이다.
1.4. Mortagages (담보 대출)
- 담보 대출은 채권과 반대되는 것처럼 보인다.
- 미래의 주택 소유자는 주택을 구입하기 위해 주택 모기지를 판매하여 즉각적인 현금을 창출하고 모기지 보유자에게 정기적으로 지불해야 할 의무가 있다.
- 표준 모기지는 만기 시 액면가를 지불하는 채권과 달리 기간 내내 매월 동일한 금액을 지불하도록 구조화되어 있다.
1.5. Annuities (연금)
- 일정 기간 동안 미리 정해진 일정이나 공식에 따라 보유자(연금수령자)에게 주기적으로 돈을 지급하는 계약
- 연금은 연금수령자가 생존하는 동안 매년 고정적으로 지급하는 구조로 되어 있음 →연금액은 가입 당시 연금수령자의 나이를 기준으로 결정됨.
- 연금은 거래되지 않으므로 증권이 아니지만 투자 기회로 간주(다른 고정 수입 증권과 동일한 역할 수행)
2. Value Formulas
2.1. Perpetual Annuities (종신 연금)
- 고정 금액을 영원히 주기적으로 지급
- 예시: 매년 1월 1일에 $1,000 평생 지급
$$P_{\infty} = \sum_{k=1}^{\infty} \frac{A}{(1+r)^k} \quad (\text{r : Interest Rate, A: Annual Payment})$$
위의 무한 등비급수를 계산하면
$$ P_{\infty} = \frac{A}{r}$$
종신 연금이 아니라 기한이 정해진 연금이라면,
$$P_{n} = \sum_{k=1}^{n} \frac{A}{(1+r)^k}$$
두 개의 종신 연금을 가지고 특정 기간의 연금의 현재 가치를 도출할 수 있는데,
1) 매년 A의 금액을 시간 1부터 무한대까지 지급
2) 매년 A의 금액을 시간 $n+1$부터 무한대까지 지급
두 번째 연금의 현재 가치를 첫 번째 연금의 현재 가치에서 빼면, 결과적으로 처음 n년 동안 매년 A의 금액을 지급하는 상품의 현재 가치를 얻을 수 있다.
$$P = \frac{A}{r} - \frac{P_{\infty}}{(1+r)^n} = \frac{A}{r} - \frac{\frac{A}{r}}{(1+r)^n} = \frac{A}{r}(1 - \frac{1}{(1+r)^n})$$
이는 경제성공학 포스팅에서 $\text{P/A Factor}$식과 동일한 결과다.
P/A Factor" target="_blank" rel="noopener" data-mce-href="http://P/A Factor">http://P/A Factor
[경제성 공학] 2. Factors: How Time and Interest Affect Money - Part 1
Notations $P$: 현재 가치 $F$: 미래 가치 $A$: 연속으로 발생하는 동일한 크기의 현금 흐름 $n$: 이자 발생 횟수 $i$: 시간 당 이자율 $t$: 시점 Future Value (미래 가치) ▶ 가장 단순한 형태: 현재 가치가 $P$
taekyounglee1224.tistory.com
3. Bonds (채권)
3.1. 채권이란?
- 채권 발행자가 지정된 이자율에 따라 채권 보유자에게 돈을 지급해야 하는 의무.
- 채권은 고정 수입 증권 중 가장 큰 금전적 가치를 나타내며 이러한 증권 중 가장 유동성이 높다.
- 일반적으로 만기일에 특정 금액(Face Value)을 지급.
- 대부분의 채권은 정기적인 이자를 지급 (Coupons)
(1) Coupons
- 마지막 쿠폰 날짜는 만기일에 해당하므로 최종 결제 금액은 액면가에 쿠폰 금액을 더한 금액과 동일하다.
- 쿠폰 금액은 액면가의 백분율로 표시된다.
- 예시: 예: 액면가 1,000원의 9% 쿠폰 채권은 연 90원의 쿠폰이 있다.
- 쿠폰 사이의 기간은 1년 미만일 수 있다.
(2) Issuing and Trading Bonds
- 발행자는 처음에 채권을 판매하여 즉시 자본을 조달 한 다음 규정 된 지불을 할 의무가 있다.
- 채권은 일반적으로 일반적인 이자율에 가까운 이자율로 발행되므로 액면가에 가까운 가격으로 판매.
- 시간이 지남에 따라 채권은 액면가와 다른 가격으로 자주 거래.
- 대부분의 채권은 경매 또는 거래소를 통해 판매 ➔ 가격은 시장에 의해 결정되므로 지속적으로 변동될 수 있다.
(3) Quality Ratings
- 채권은 고정 수입원을 약속하지만 발행자가 재정적 어려움을 겪거나 파산하면 채무 불이행이 발생할 수 있다.
- 채권은 신용평가 기관(예: 무디스, 스탠다드앤드푸어스)에서 등급을 매긴다.
- 미국 재무부 증권은 채무 불이행 위험이 없는 것으로 간주되기 때문에 등급이 매겨지지 않는다.
3.2. Yields (수익률)
(1) Coupon Rate (표면 금리)
- Coupon Rate는 채권 액면가를 기준으로 채권 보유자에게 지급되는 연간 이자 소득의 금액이다.
- 채권 발행자는 채권 보유자의 초기 투자금, 즉 채권의 액면가가 채권 보유자에게 반환되는 만기까지 주기적으로 이자를 지급
(2) Bond Yield (채권 수익률)
- 결제 구조에 내포된 이자율
- 지급 흐름의 현재 가치(쿠폰 지급 포함)가 현재 가격과 정확히 일치하는 이자율
- (쿠폰 지급 포함)의 현재 가치가 현재 가격과 정확히 일치하는 이자율
Yield to Maturity (만기 수익률)
- 수익률은 항상 연간 기준으로 제시된다.
- YTM은 현재 가격에서 채권의 IRR (내부 수익률)이다.
$$0 = x_0 + \frac{x_1}{1 + r} + \frac{x_2}{(1 + r)^2} + \cdots + \frac{x_n}{(1 + r)^n}$$
★Coupon Rate와 YTM의 차이점:
- 표면금리 채권 보유자가 매년 실제로 받는 이자 금액을 나타내며, 만기 수익률은 채권을 만기까지 보유한다고 가정할 때 예상되는 총 수익률이다.
- 표면금리는 고정된 상태로 유지되지만 만기 수익률은 변동될 수 있다.
- 만기 수익률을 계산할 때는 이자율과 채권 가격의 상승 또는 하락을 고려한다.
(3) Bond Price (채권 가격, 발행가)

매년 일정한 고정 수익 $C(\text{coupon}) = c\times F$가 발생하고, 만기에 액면가 $F$를 돌려받는다고 가정할 때, 채권의 현 시점 발행가 $P$는
$$P = \frac{F}{(1 + \frac{\lambda}{m})^n} + \sum_{k=1}^{n} \frac{C}{m} \left(1 + \frac{\lambda}{m} k\right) \quad (\lambda : \text{Yield to Maturity})$$
$\sum$ 부분을 정리하면
$$P = \frac{F}{(1 + \frac{\lambda}{m})^n} + \frac{C}{\lambda} (1- \frac{1}{(1+\frac{\lambda}{m})^n})$$
로 쓸 수 있다.
이 때, 만약 $\lambda = c$, 즉 만기수익률이 표면금리와 같다면?
$$P = \frac{F}{(1 + \frac{\lambda}{m})^n} + \frac{\lambda \times F} {\lambda} (1- \frac{1}{(1+\frac{\lambda}{m})^n}) = F$$
발행가가 액면가와 동일하게 나온다!
가격, 수익률, 이자율, 만기까지의 시간 간의 관계는 채권 포트폴리오 구성에 동기를 부여하고 채권의 이자율 위험 특성을 이해하는 데 도움이 된다. 채권의 수익률은 채권의 가격이 변할 때만 변할 수 있는데, 즉 수익률이 움직이면 가격도 그에 따라 움직이는 경향을 보인다.
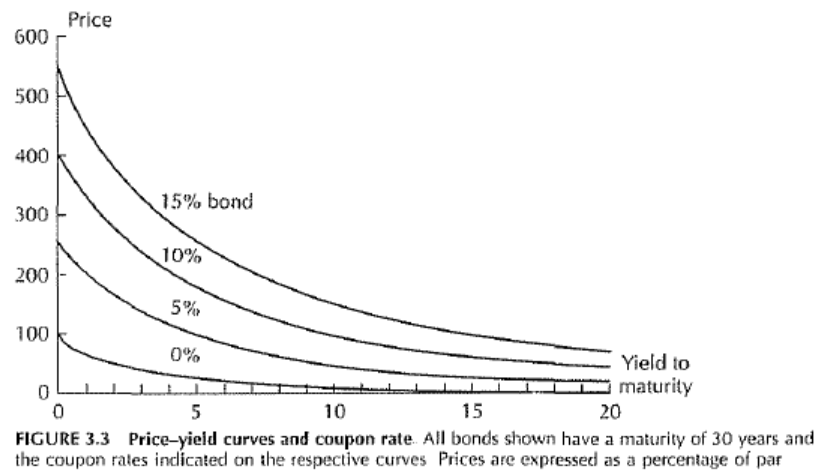
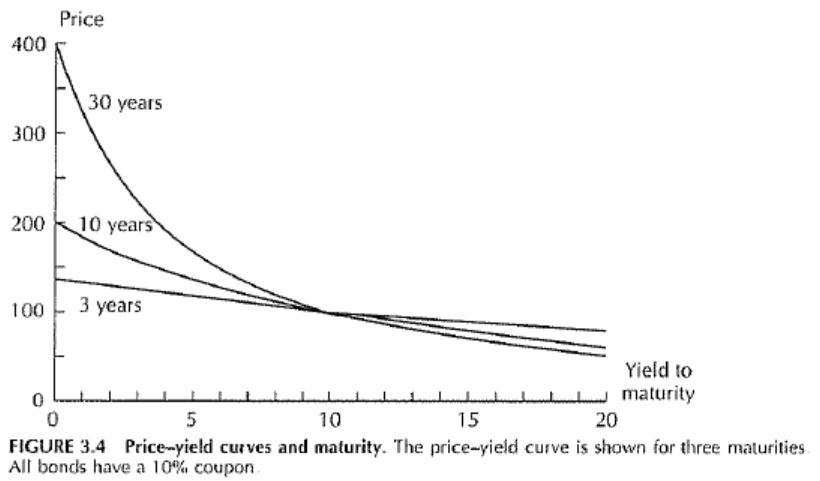
위 두 그래프를 살펴보자. 두 그래프 모두 만기수익률 대비 채권 가격의 관계를 나타낸다.
왼쪽 그래프의 경우, coupon rate가 변함에 따라 수익률-가격 곡선이 어떻게 변하는지를 보여준다. coupon rate가 높을수록 그래프의 기울기가 커짐을 볼 수 있는데, 이는 표면금리가 높을 수록 가격의 변동 폭이 더 큼을 보여준다.
오른쪽 그래프의 경우, 동일한 coupon rate를 가진 채권이 만기에 따라 어떻게 형태가 달라지는지를 보여준다. 만기가 길수록 기울기가 커지는 것을 보아, 만기가 긴 채권일수록 가격 변동이 더 크다는 것을 알 수 있다. 또한, 세 곡선 모두 (10,100)에서 만나는데, 이 지점이 만기수익률과 표면금리가 같아져, 발행가가 액면가와 동일하게 나오는 지점이다.
3.3. Duration
만기가 긴 채권은 만기가 짧은 채권보다 가격-수익률 곡선이 더 가파르다. 그러나 만기 자체가 금리 민감도의 완전한 정량적 척도는 아니다. 민감도를 직접적으로 측정하기 위한 척도로 Duration이 쓰인다.
Duration이란, 채권 투자에서 자금이 회수되는 평균 기간을 의미한다. 다시 말해, 채권에 투자한 원금을 회수하는데 걸리는 기간이다. 얼핏 만기랑 같은 것이 아닌가 하는 생각이 들 수 있지만, 만기와는 차이가 있다.
금융공학 2장 포스팅과 경제성공학 포스팅에서 현재가치와 미래가치에 대해 설명한 적이 있다. 예를 들어, 1년 후 1000원의 가치는 시장금리가 10%일 때, 현재 909.1원의 가치를 갖는다. 따라서 듀레이션은 이자와 원금의 현재가치를 반영하여 계산하는 가중평균회수기간이다.
$$ D = \frac{PV_{t1} t1 + PV_{t2} t2 + \cdots + PV_{tn} tn}{PV_{t1} + PV_{t2} + \cdots + PV_{tn}} = \frac{PV_{t1} t1 + PV_{t2} t2 + \cdots + PV_{tn} tn}{PV}$$
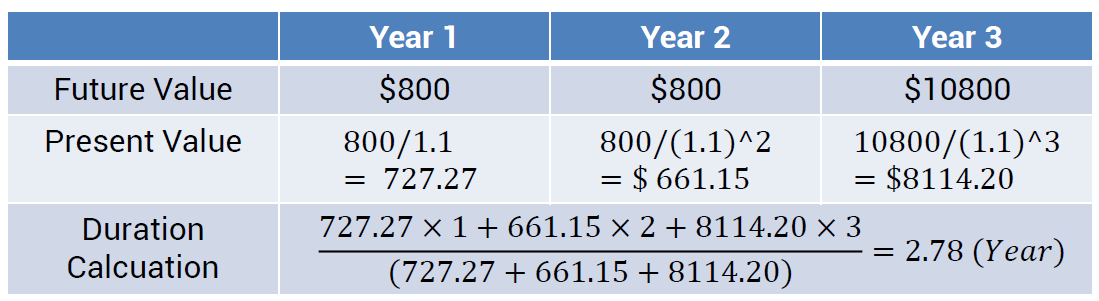
듀래이션 공식을 보면 각 시점의 현재가치에 시점이 가중치로 곱해진 것을 볼 수 있다. 같은 금액의 돈이라도 늦게 받을 수록 할인율이 크게 적용되므로 현재가치는 낮아진다. 따라서 현재가치가 낮아지는 것을 방지하기 위해 더 늦은 현금 흐름에 더 큰 가중치를 부여한다.
즉, 늦은 현금 흐름일수록 현재 가치에 더 큰 영향을 미치게 되고, 이자율 변동에 더 민감할 수밖에 없다. 따라서 장기 채권의 경우(듀레이션이 긴 경우) 이자율 리스크가 크다고 해석할 수 있다.
위 표의 예시를 보면, 채권이 2.78년의 듀레이션을 갖는데, 이는 3년 간 3번 발생하는 각각의 현금 흐름의 현재 가치를 고려했을 때, 평균적으로 2.78년 후에 투자금을 '실질적으로' 회수하는 것과 같은 효과를 내는 것을 의미한다. 또한 채권의 가격은 시장 이자율이 변할 때, 평균적으로 2.78년치 현금 흐름의 변화와 동등한 영을 받는다는 것을 뜻하기도 한다.
정리하면, 듀레이션이 갖는 의미는
- 투자자가 투자금을 회수하게 되는 평균 기간
- 채권가격이 시장 이자율에 민감하게 변동하는 정도 (위의 경우는 이자율 1% 당 2.78%만큼 변동)
듀레이션을 계산할 때 보통 Macaulay Duration 공식을 사용한다.
$$D = \frac{\sum_{k=1}^{n} \frac{k}{m} \cdot \frac{c_k}{(1 + \frac{\lambda}{m})^k}}{PV}$$
이 때, YTM 대신 period 당 yield $y$를 이용해 공식을 표현하면,
$$D = \frac{1 + y}{my} - \frac{1 + y + n(c - y)}{mc((1 + y)^n - 1) + my}$$
3.4. Sensitivity (민감도)
Duration이 채권의 민감도와 연관되는 것을 알았는데, 이를 계산하는 방법이 뭘까?
채권의 민감도란 결국 이자율 변화에 따른 채권의 가격 변화를 의미하는 것이므로 우리는 채권의 가격 변화율을 유도해 낼 필요가 있다.
각 시점의 현재가치를 수익률에 대해 미분하면 다음과 같다.
$$PV_k = \frac{c_k}{(1 + \frac{\lambda}{m})^k}$$
$$\frac{\mathrm{d} PV_k}{\mathrm{d} \lambda} = -\frac {\frac{k}{m}}{1 + \frac{\lambda}{m}}PV_k$$
이를 모든 $k$에 대해 총합을 구하면
$$\frac{\mathrm{d} P}{\mathrm{d} \lambda} = -\sum_{k=1}^{n}\frac {\frac{k}{m}}{1 + \frac{\lambda}{m}}PV_k = -\frac{D}{1+\frac{\lambda}{m}}P = -D_MP$$
여기서 $D_M$은 수정 듀레이션으로, $D_M = \frac{D}{1+\frac{\lambda}{m}}$와 같이 표현된다.
식을 다시 정리하면.
$$ \frac{\mathrm{d} P}{\mathrm{d} \lambda} = -D_MP$$
$$ \frac{\mathrm{d} P}{\mathrm{d} P} = -D_M\lambda$$
이를 평균변화율로 취하면
$$\frac{\Delta P}{P} = -D_M\Delta{\lambda}$$
로 표현할 수 있으며, 가격 변화율인 $ \frac{\Delta P}{P}$가 채권의 민감도에 해당하는 부분이다.
'금융공학' 카테고리의 다른 글
| [금융] 거시 경제와 금융 (2) | 2024.07.20 |
|---|---|
| [Quant] Term Structure of Interest Rates (이자율의 기간구조) (0) | 2024.04.19 |
| [Quant] Nominal and Effective Interest Rates (0) | 2024.03.24 |
| [Quant] Factors: How Time and Interest Affect Money - Part2 (2) | 2024.03.23 |
| [Quant] The Basic Theory of Interest (2) | 2024.03.22 |